It's easy to create rich visualizations of ice and snow thickness, growth, melt, and temperature profile using SIMB3 data. In this tutorial, we’ll show you how to do it using the Python programming language.
Before we get started, you'll need:
An SIMB3 datasheet (or sample below) A code editor of choice (we recommend Visual Studio) If you'd like to skip the tutorial and get straight to plotting, you can download the script that we build in this tutorial here:
A quick introduction
One of the best parts about working with SIMB3 data is that the results are highly visual. With the surface and bottom rangefinder data alone we can see how the ice change thickness through the season. By incorporating data from the vertical temperature string, we can examine the vertical conductive heat flux. If we combine all three measurements, we create a comprehensive picture of the ice state through time that we refer to as a plot a mass balance plot.
The mass balance plot
A mass balance plot shows ice and snow growth, melt, and internal temperature on a single, easily understandable figure (Figure 1). On the x-axis is time and on the y-axis is thickness or depth. As the ice grows and melts, the distances recorded by the SIMB3 surface and bottom rangefinders lengthen and shorten. With a little knowledge of the SIMB3 dimensions and the deployment conditions, we can turn these distances into ice and snow thickness values. Over time, changes in these values represent ice and snow growth and melt.
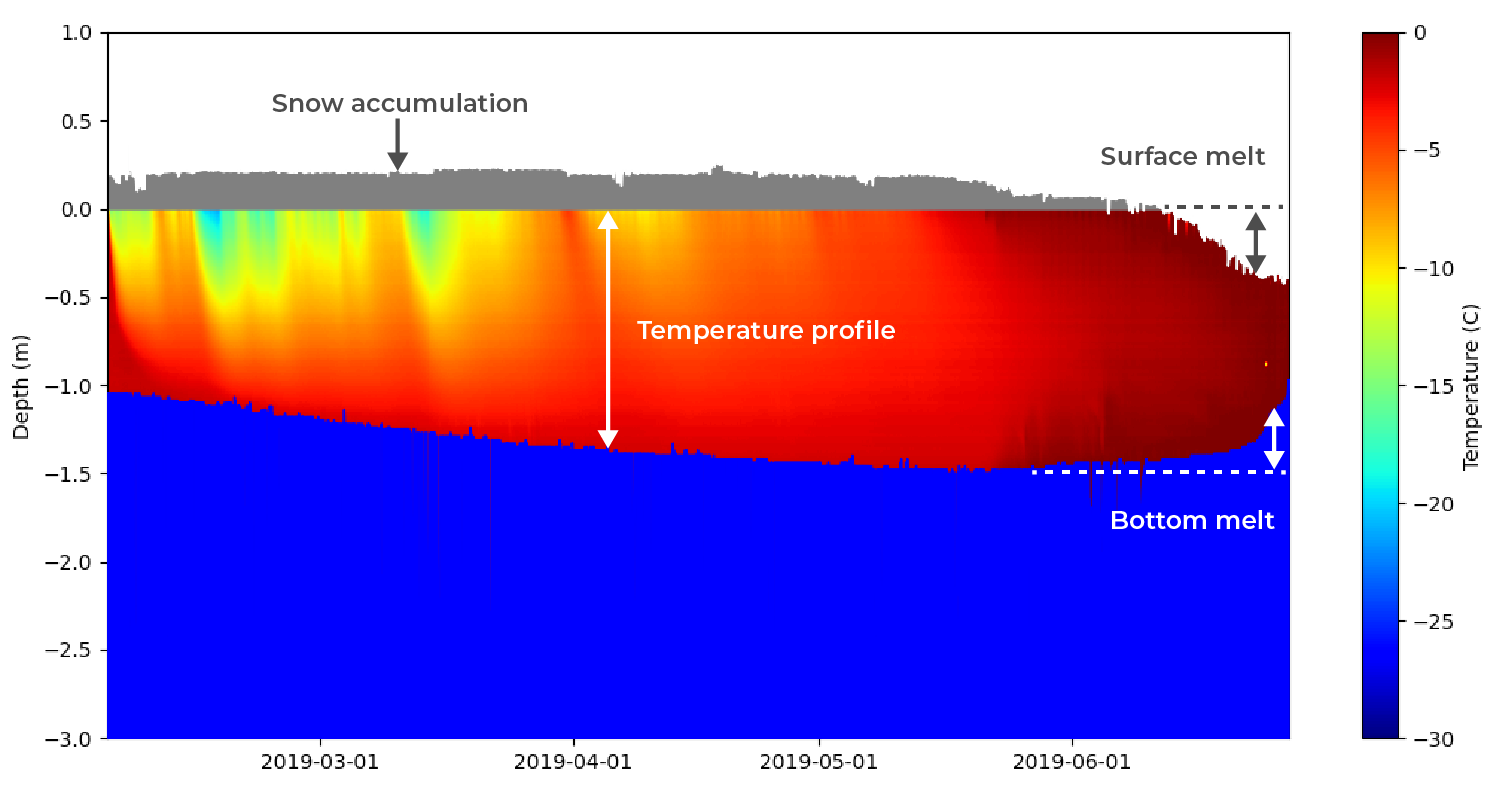Figure 1: From the mass balance plot you can easily determine ice growth, melt, snow accumulation, and temperature profile visually. Because SIMB3 independently measures surface and bottom position, surface and bottom melt can be distinguished.Time-series line plots
SIMB3 is also equipped with sensors that measure upper-ocean temperature, battery voltage, and meteorological data such as air temperature and barometric pressure. Creating these plots is straightforward compared to the mass balance plot, so we're not going to cover it in this article.
Getting started with Python
Okay, let's get right into. From the Real Time Data portal, navigate to the page for the SIMB3 which you’d like to analyze. Click the green “Download CSV” button to download the most recent datasheet for the instrument.
Create a new Python file
Inside of your code editor or terminal, navigate to a directory where you'd like to store your files for this project. Create a new file and give it a name and .py extension. We created a directory named SIMB3_Python and a file named massBalancePlot.py. While not required, I'd recommend moving your freshly downloaded datasheet into this directory.
In a MacOS/Linux terminal:
cd ~
mkdir SIMB3-Python
cd SIMB3-Python
touch massBalancePlot.py
Installing required libraries
We'll be using the Numpy, Pandas, and Matplotlib libraries to structure, manipulate, and eventually plot our data. To import them, open your Python file and add the following lines at the very top.
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
If you haven't used any or all of these libraries before, you will need to install them. This is done simply using pip3 install.
pip3 install numpy pandas matplotlib
Creating the mass balance plot function
For the mass balance plot, copy the following code directly below your import statements. Don't worry, we'll explain the whole thing block-by-block below.
def plot_simb(dtc: np.ndarray, surface_distance, bottom_distance, timestamp, initial_snow_depth, distance_between_rangefinders):
#calculate height of surface rangefinder above the ice surface
height_above_ice = surface_distance[0] + initial_snow_depth
#create arrays that store values for each timestamp
snow_height = height_above_ice - surface_distance
ice_thickness = distance_between_rangefinders - height_above_ice - bottom_distance
ice_thickness = - ice_thickness #make negative for plotting because it's below waterline
#define temperature string position (height above ice)
temp_string_length = 3.84 #standard SIMB3 temperature string has 2 cm spacing and 192 thermistors
temp_string_offset = 0 #the axial distance between the surface rangefinder and the first thermister on the DTC
temp_string_top = height_above_ice - temp_string_offset #distance from the top of the ice to the first thermistor in the temperature string
temp_string_bottom = temp_string_length - temp_string_top
temp_string_bottom = temp_string_bottom * (-1) #make negative for plotting
#shift excel serial date (1900 epoch) to the Python 1970 epoch by adding the number of days between 01/01/1900 and 01/01/1970
#then subtract 1 to account for the famous 1900 excel leap year timestamp bug
timestamp = timestamp - 25568 - 1
#set plot bounds
upper_bound = 1
lower_bound = -3
#create mass balance plot
fig, ax = plt.subplots()
im = ax.imshow(dtc, cmap='jet', vmin=-30, vmax=0, extent=[timestamp[0], timestamp[-1], temp_string_bottom, temp_string_top],
aspect='auto', zorder=0) #format ice temperature heatmap from dtc (temperature string) data
plt.colorbar(im, ax=ax, label='Temperature (C)')
#color in between the lines
ax.fill_between(timestamp, snow_height, 0, color="grey", zorder=1) #plot snow height on top of ice
ax.fill_between(timestamp, temp_string_top, snow_height, color='white', zorder=2) #create whitespace above snow
ax.fill_between(timestamp, ice_thickness, lower_bound, color='b', zorder=3) #plot lower boundary of ice
#bound and label y axis
ax.set_ylim(lower_bound, upper_bound)
plt.ylabel('Depth (m)')
#format x-axis as date
formatter = mdates.DateFormatter("%Y-%m-%d")
ax.xaxis.set_major_formatter(formatter)
#only label each month
locator = mdates.MonthLocator()
ax.xaxis.set_major_locator(locator)
plt.show()
Taking a look at the function declaration, we see that it takes values from the temperature string (dtc: np.ndarray), the surface rangefinder (surface_distance), the bottom rangefinder (bottom_distance), the time stamp (timestamp), the initial snow depth (initial_snow_depth), and the rangefinders distance (distance_between_rangefiners) as inputs.
Of these inputs, the surface_distance, bottom_distance, timestamp are 1D arrays of length 1 x N, where N is the length of datasheet (often the number of transmissions from the buoy). The temperature string array (dtc: np.ndarray) is 2D with a size of 192 x N. The initial_snow_depth and distance_between_sounders values are both scalars.
Define reference height from ice surface
We tried to give the variables in this function intuitive names, but let's still go through it block-by-block to make sure there's no confusion. In the first row, we calculate the fixed distance between the surface rangefinder and the ice surface by summing the first value in the surface_distance array (i.e., the value immediately after the buoy was deployed) and the initial snow height. You can also declare this value manually using measurements from deployment.
#calculate height of surface rangefinder above the ice surface
height_above_ice = surface_distance[0] + initial_snow_depth
Snow height and ice thickness
We then create two arrays that define the snow height (i.e., the snow thickness) and the ice thickness. The snow height is simply the height of the surface rangefinder above the ice (does not change once the SIMB3 is frozen in) minus the reading from the surface rangefinder.
#create arrays that store values for each timestamp
snow_height = height_above_ice - surface_distance
ice_thickness = distance_between_rangefinders - height_above_ice - bottom_distance
ice_thickness = - ice_thickness #make negative for plotting because it's below waterline
We then compute the ice thickness by subtracting the height of the surface rangefinder above the ice (height_above_ice) and the bottom rangefinder value (bottom_distance from the total distance between rangefinders, distance_between_rangefinders. For a standard SIMB3, distance_between_rangefinders = 4.051 meters.
Temperature string height reference
Moving along to the second block, we create several variables which define the position of the temperature string relative to the SIMB3 surface rangefinder and to the ice surface.
#define temperature string position (height above ice)
temp_string_length = 3.84 #standard SIMB3 temperature string has 2 cm spacing and 192 thermistors
temp_string_offset = 0 #the axial distance between the surface rangefinder and the first thermister on the DTC
temp_string_top = height_above_ice - temp_string_offset #distance from the top of the ice to the first thermistor in the temperature string
temp_string_bottom = temp_string_length - temp_string_top
temp_string_bottom = temp_string_bottom * (-1) #make negative for plotting
The standard SIMB3 Bruncin digital temperature string is 3.84 meters long and measures temperature at 2 cm intervals along the length (192 total values). During buoy manufacturing, the position of the first thermistor is placed 0.2 cm below the surface rangefinder. After installation and freeze-in, this becomes a fixed position above the ice (temp_string_top).
The temperature string bottom (i.e., the distance between the ice surface and the final thermistor on the chain) is simply the length of the temperature string minus the height of the first thermistor above the ice surface.
Realign Excel timestamp
While this is not strictly necessary, to have dates to plot along the x-axis, we need to realign the Excel serial date to the 1970 epoch used by Python. To do this, just add the number of days (including leap years!) between 01/01/1900 and 01/01/1970. Note that you must also subtract one extra day to account for the infamous Excel leap year bug. For more on how dates are handled in excel, check this out.
#shift excel serial date (1900 epoch) to the Python 1970 epoch by adding the number of days between 01/01/1900 and 01/01/1970
#then subtract 1 to account for the famous 1900 excel leap year timestamp bug
timestamp = timestamp - 25568 - 1
Plot window parameters
Finally, we set the bounds for our plot window. For most buoys, 1 m above the ice surface and 3 meters below the surface is good.
#create mass balance plot
fig, ax = plt.subplots()
im = ax.imshow(dtc, cmap='jet', vmin=-30, vmax=0, extent=[timestamp[0], timestamp[-1], temp_string_bottom, temp_string_top],
aspect='auto', zorder=0) #format ice temperature heatmap from dtc (temperature string) data
plt.colorbar(im, ax=ax)
Plot temperature string values
We're now ready to assemble the mass balance figure. We'll start by defining a plt.subplots() object, and then we'll pass it our temperature string data.
Here, the imshow() function takes in our digital temperature string array (dtc) and the bounds of the mesh over which we want to plot (in this case, on the x-axis from the first to last entry in timestamp and on the y-axis from temp_string_bottom to temp_string_top).
imshow() plots the temperature string data and plt.colorbar(im, ax=ax) adds a colorbar with bounds defined by vmin and vmax. Both vmin and vmax should be set so that they encompass any temperature value present in the temperature string array.
Plot rangefinder values
As the final step in the creation of our mass balance plot function, we'll fill in the regions of our plot corresponding to air, snow, and water using the rangefinder values. This is straightforward using the fill_between() function.
#color in between the lines
ax.fill_between(timestamp, snow_height, 0, color="grey", zorder=1) #plot snow height on top of ice
ax.fill_between(timestamp, temp_string_top, snow_height, color='white', zorder=2) #preate whitespace above snow
ax.fill_between(timestamp, ice_thickness, lower_bound, color='b', zorder=3) #plot lower boundary of ice
We can then set the y-limits of the plot, format the x-axis as a date, and command the plot to show when the plot_simb function is called.
#bound y axis
ax.set_ylim(lower_bound, upper_bound)
#format x-axis as date
formatter = mdates.DateFormatter("%Y-%m-%d")
ax.xaxis.set_major_formatter(formatter)
#only label each month
locator = mdates.MonthLocator()
ax.xaxis.set_major_locator(locator)
Calling the mass balance plot function
To call our mass balance plot, we need to parse our CSV datasheet and pass the required parameters into the plot_simb() function. To do this, let's make an another function that takes our data path, initial snow depth, and plot range in as arguments and then calls plot_simb().
def plot_from_csv(path_to_data: str, initial_snow_depth: float, plot_range):
#try to read csv at input location
try:
simb_df = pd.read_csv(path_to_data,skiprows=plot_range[0], nrows=plot_range[1]) #create pandas dataframe from csv
timestamp = simb_df.time_stamp.to_numpy() #extracts time stamp from simb_df dataframe, converts to numpy array
except FileNotFoundError:
print('Invalid Path, please check file location.')
return
# Distance between sounders in meters, used for bounding the Ice Mass Balance Plot
sounder_dist = 4.051
# Extract relevant data from dataframe, convert to numpy array
snow_dist = simb_df.surface_distance.to_numpy() # distance from upper sounder to snow
water_depth = simb_df.bottom_distance.to_numpy() # distance from lower sounder to bottom of ice
dtc_values = simb_df.filter(like='dtc_values_').to_numpy().T # temperature string data at 2 cm intervals
# Call plot function for ice mass balance plot
plot_simb(dtc_values, snow_dist, water_depth, timestamp, initial_snow_depth, sounder_dist)
This function just extracts data from our datasheet as Pandas dataframes and passes it to our plot_simb() function. When using it, the only thing to watch out for is the plot_range parameter which cannot be longer than our datasheet (i.e., it cannot have more rows than our datasheet).
As the final line in our script, we call our our plot_from_csv() function. For the SIMB3sampleDataSheet.csv used in this tutorial, we'll use 0.2 m as the initial_snow_depth and [0 3378] as the plot_range. Note: you'll need to use the correct path to your datasheet if it's not in your working directory.
plot_from_csv(r'SIMB3sampleDataSheet.csv', .2, [0, 3378])
Running the script
To run the script and create the plot, go back to your terminal and run:
python3 massBalancePlot.py
You should see the plot in Figure 2 appear.
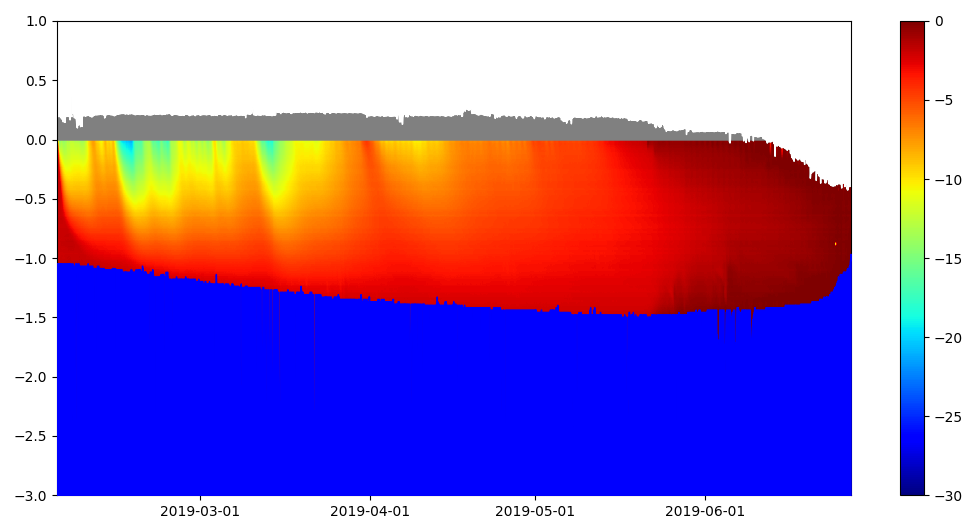
Figure 2: Our final mass balance plot, generated using open-source software.
Just like that, we've created a mass balance plot from SIMB3 data using Python! Because we build this script using functions, it's easy to call for multiple SIMB3 datasets or for multiple iterations of the same dataset.
This tutorial was written by Henry Prestegaard and Cameron Planck.